20300 - Matemàtica Discreta. Grup 01,02, 03, 10 i 11
Looking for 20300 - Matemàtica Discreta. Grup 01,02, 03, 10 i 11 test answers and solutions? Browse our comprehensive collection of verified answers for 20300 - Matemàtica Discreta. Grup 01,02, 03, 10 i 11 at ad.uib.es.
Get instant access to accurate answers and detailed explanations for your course questions. Our community-driven platform helps students succeed!
La relació 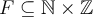 F\subseteq \mathbb{N}\times\mathbb{Z} definida per
F\subseteq \mathbb{N}\times\mathbb{Z} definida per 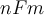 nFm si, i només si
nFm si, i només si 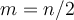 m=n/2 si
m=n/2 si 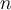 n és parell o
n és parell o 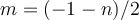 m=(-1-n)/2 si
m=(-1-n)/2 si 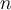 n és imparell:
n és imparell:
0%
❌
0%
0%
0%
View this question
Considerau el conjunt 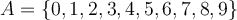 A=\{0,1,2,3,4,5,6,7,8,9\} i la familia de subconjunts
A=\{0,1,2,3,4,5,6,7,8,9\} i la familia de subconjunts 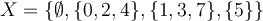 X=\{\emptyset,\{0,2,4\},\{1,3,7\},\{5\}\}. Quina o quines de les afirmacions següents és vertadera?
X=\{\emptyset,\{0,2,4\},\{1,3,7\},\{5\}\}. Quina o quines de les afirmacions següents és vertadera?
0%
❌
❌
0%
0%
View this question
Considerau els multiconjunts A={1,1,2,2,2,2,3,3,4,4,5,5} i B={1,1,2,2,3,3,4,4,4,5,5,5}. Què val el cardinal de la seva unió?
View this question
Sigui 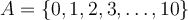 A=\{0,1,2,3,\ldots,10\}. Quina d'aquestes afirmacions és certa?
A=\{0,1,2,3,\ldots,10\}. Quina d'aquestes afirmacions és certa?
0%
❌
0%
0%
0%
View this question
Donats 3 conjunts  A,B,C, considerau les igualtats: (a)
A,B,C, considerau les igualtats: (a) 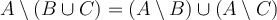 A\setminus (B\cup C)=(A\setminus B)\cup (A\setminus C) (b)
A\setminus (B\cup C)=(A\setminus B)\cup (A\setminus C) (b) 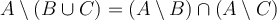 A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C). Quina de les afirmacions següents és vertadera?
A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C). Quina de les afirmacions següents és vertadera?
0%
❌
0%
0%
View this question
Considerau el conjunt 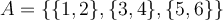 A=\{\{1,2\},\{3,4\},\{5,6\}\}. Quina o quines de les afirmacions següents són vertadera? Marcau les vertaderes.
A=\{\{1,2\},\{3,4\},\{5,6\}\}. Quina o quines de les afirmacions següents són vertadera? Marcau les vertaderes.
0%
0%
0%
0%
✅
View this question
Considerau sobre el conjunt 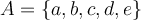 A=\{a,b,c,d,e\} la relació
A=\{a,b,c,d,e\} la relació 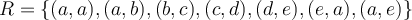 R=\{(a,a),(a,b),(b,c),(c,d),(d,e),(e,a),(a,e)\}. Quina o quines de les afirmacions següents és vertadera?
R=\{(a,a),(a,b),(b,c),(c,d),(d,e),(e,a),(a,e)\}. Quina o quines de les afirmacions següents és vertadera?
❌
❌
❌
❌
❌
✅
View this question
Sigui A el conjunt dels alumnes de matemàtica discreta. Definim la relació 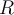 R en A com
R en A com  aRb si, i només si, hi ha alguna assignatura del primer semestre que tant
aRb si, i només si, hi ha alguna assignatura del primer semestre que tant  a com
a com 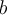 b hagin aprovat. És R una equivalència sobre A?
b hagin aprovat. És R una equivalència sobre A?
✅
❌
View this question
Want instant access to all verified answers on ad.uib.es?
Get Unlimited Answers To Exam Questions - Install Crowdly Extension Now!